强化学习(Reinforcement Learning, RL)是一种机器学习方法。给定一系列的奖励和惩罚,学习未来要执行什么样的动作。
强化学习不是人工智能领域独有的概念。心理学中的强化学习理论源于行为主义心理学,特别是由B.F. Skinner等学者发展的操作性条件作用(Operant Conditioning)。在心理学背景下,强化学习关注的是有机体如何通过与环境的交互来学习新的行为。
心理学领域强化学习的例子:
- 训练宠物,当宠物照指令行动时,给它一块小零食作为奖励
- 学生主动回答问题或提出见解,老师表扬该学生,并给予额外的积分或奖励
- 孩子没有按时完成家庭作业,父母决定如果孩子未能按时完成作业,就不能玩电子游戏或使用手机等设备;一旦孩子开始按时完成家庭作业,父母就不再限制他们使用电子设备的时间
人工智能领域知名强化学习项目:
- 围棋(AlphaGo):DeepMind 开发的 AlphaGo 程序在2016年以4比1的总比分战胜了世界冠军李世石,随后又在中国乌镇围棋峰会上以3比0的成绩战胜了当时的世界第一柯洁。
- 星际争霸Ⅱ(AlphaStar):AlphaStar 是由 DeepMind 开发的一款人工智能系统,专为玩《星际争霸 II》设计。这款即时战略游戏因其复杂的决策过程、庞大的动作空间以及部分可观测性而闻名,被认为是衡量 AI 在处理复杂动态环境能力的一个重要基准。2019年 AlphaStar 分别以5比0的成绩击败了两位职业选手。
- 宇树科技四足机器人 B2-W:能够站立、跳跃、侧空翻、爬山、涉水、甚至载人的“狗”形态机器人。
其它机器学习方法还有监督学习和非监督学习,强化学习与其它方法最重要的区别:强化学习评估动作的价值作为训练信息,而非给出正确的行动指导来作为训练信息。纯指导性的反馈(打标签)是监督学习的特征。
马尔可夫决策过程(Markov Decision Process)
马尔可夫决策过程(Markov Decision Process,简称 MDP)是强化学习中用于描述决策制定过程的基本框架。MDP 是一种数学模型,用于描述在一个系统中做出一系列决策的过程,其中每个决策都可能改变系统的状态。MDP 在强化学习、机器人学、自动化控制等领域中有广泛应用。MDP 用状态、动作和它们的奖励来表示决策制定的模型。
马尔可夫性质
马尔可夫性质(Markov Property)是概率论和随机过程中的一个重要概念,尤其在马尔可夫链(Markov Chain)和马尔可夫决策过程中广泛使用。马尔可夫性质的核心思想是,系统的未来状态仅依赖于当前状态,而不依赖于过去的历史状态。或者说,当前状态能够包含所有对未来决策或状态预测有用的信息。
象棋是符合马尔可夫性质的。以象棋为例,象棋第 n + 1 步的棋盘状态由第 n 步棋盘状态决定,与第 n - 1 步棋盘状态无关。无论第 n 步棋盘状态是如何从第 n - 1 步棋盘状态下出来的,都不会影响对 n + 1 步的判断。
不符合马尔可夫性质的任务以股票市场为例。在股票市场中,股价的变化可能不仅受到当前价格的影响,还会受到历史价格趋势、公司业绩报告、宏观经济指标以及各种内外部因素的影响。因此,预测股票未来的价格走势不能仅仅基于当前的价格。
满足马尔可夫性质的强化学习任务称为马尔可夫决策过程(Markov Decision Process, MDP),如果状态和动作空间是有限的,称为有限马尔可夫决策过程。
在强化学习中马尔科夫性质很重要,因为假设了决策和价值是仅基于当前状态的函数。
MDP 的定义
MDP 由以下几个组成部分构成:
- 状态集合 ( S ):表示系统可能处于的所有状态的集合。
- 动作集合 ( A ):表示在每个状态下可以采取的所有动作的集合。
- 转移概率 ( P ):表示在状态 ( s ) 下采取动作 ( a ) 后转移到状态 ( s' ) 的概率,记为 ( P(s'|s, a) )。
- 奖励函数 ( R ):表示在状态 ( s ) 下采取动作 ( a ) 后获得的即时奖励,记为 ( R(s, a) ) 或 ( R(s, a, s') )。
- 折扣因子 ( \gamma ):表示未来奖励的重要性相对于当前奖励的程度,通常 ( 0 \leq \gamma < 1 )。
MDP 的形式化表示
MDP 可以形式化地表示为五元组 ( (S, A, P, R, \gamma) ),其中:
- ( S ) 是状态集合;
- ( A ) 是动作集合;
- ( P ) 是转移概率矩阵;
- ( R ) 是奖励函数;
- ( \gamma ) 是折扣因子。
MDP 的目标
在 MDP 中,智能体的目标是找到一个策略 ( \pi ),使得从初始状态出发,智能体按照策略行动时能够最大化累积奖励。累积奖励可以用如下形式表示:
[ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t+k+1} ]
这里的 ( G_t ) 称为从时间步 ( t ) 开始的未来累积折扣奖励。
策略(Policy)
策略 ( \pi ) 定义了在给定状态下应该采取的动作。策略可以是确定性的(在每个状态下都有一个明确的动作),也可以是随机性的(在每个状态下都有一个动作的概率分布)
价值函数(Value Function)
价值函数用来评估状态的好坏。有两种主要的价值函数:
- 状态价值函数 ( V^\pi(s) ):表示在策略 ( \pi ) 下,从状态 ( s ) 开始时所能获得的预期未来累积折扣奖励。
- 动作价值函数 ( Q^\pi(s, a) ):表示在策略 ( \pi ) 下,从状态 ( s ) 开始采取动作 ( a ) 后所能获得的预期未来累积折扣奖励。
MDP 的解决方案
MDP 的解决方案通常涉及以下几个步骤:
- 策略评估(Policy Evaluation):给定一个策略 ( \pi ),计算其对应的状态价值函数 ( V^\pi ) 或动作价值函数 ( Q^\pi )。
- 策略改进(Policy Improvement):给定一个策略 ( \pi ),找到一个新的策略 ( \pi' ),使得在所有状态下 ( \pi' ) 至少不比 ( \pi ) 差,即 ( V^{\pi'}(s) \geq V^\pi(s) )。
- 策略迭代(Policy Iteration):交替进行策略评估和策略改进,直到策略收敛。
- 价值迭代(Value Iteration):直接通过迭代更新价值函数来找到最优策略。
示例
下面是一个简单的 MDP 示例,说明如何定义一个 MDP 并解决问题:
假设有一个迷宫游戏,智能体需要从起点到达终点。迷宫中有多个状态,智能体可以向四个方向移动(上、下、左、右)。每个状态都有一定的奖励,到达终点会有较高的奖励。
- 状态集合 ( S ):迷宫中的每一个位置。
- 动作集合 ( A ):向上、向下、向左、向右移动。
- 转移概率 ( P ):在每个状态下采取动作后的转移概率(假设动作总是成功)。
- 奖励函数 ( R ):在每个状态下的即时奖励。
- 折扣因子 ( \gamma ):未来奖励的重要性。
使用策略迭代或价值迭代算法可以找到最优策略,即从任意状态出发到达终点的最佳路径。
MDP 是强化学习的基础,通过对 MDP 的研究和解决,可以扩展到更复杂的强化学习问题。
Q-Learning
学习函数 ( Q(s, a) ) 的方法,能够评估在状态 ( s ) 下执行动作 ( a ) 的价值。
方法:
- 从 ( Q(s, a) = 0 ) 开始(所有状态和动作价值为 0)
- 当采取动作并获得奖励后:
- 根据当前收益和未来期望收益评估 ( Q(s, a) ) 的价值
- 结合旧的评估值和新的评估值更新 ( Q(s, a) )
更新规则
每次在状态 ( s ) 执行动作 ( a ) 观察到奖励 ( r ) ,更新:
[ Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma \max_{a'} Q(s', a') - Q(s, a) \right] ]
其中:
- ( r ) 当前动作获得的奖励
- ( \gamma \max_{a'} Q(s', a') ) 未来预期的奖励
- ( a' ) 表示接下可执行的动作
- ( \max_{a'} ) 所有可执行的动作中取最大奖励值
- ( \gamma ) 未来预期奖励的权重
Greedy Decision-Making
- 处于状态 ( s ) 时,选择最大 ( Q(s, a) ) 值的动作 ( a )。
每次决策选择已知的最优解可以最大化短期利益,但不会保证长期利益。
ε-Greedy
- 设置 ( ε ) 值为随机动作的概率。
- 以 ( 1 - ε ) 的概率为选择最佳动作的概率。
- 以 ( ε ) 的概率为选择随机动作的概率。
ε-Greedy 是在决策过程中以一定的概率随机选择一个动作,而不是只选择最佳动作,使得决策过程引入探索的能力,有益于找寻可能的更佳适合的解,从而提升长期收益。ε-Greedy 常在学习初期设置一个较大的值,鼓励探索,随着训练的进行,ε逐渐减小,鼓励利用训练过的知识,提高收益。
平衡利用和探索
平衡利用(exploiting)和探索(exploration)是强化学习中的一个重要课题。“利用”是根据已有的知识选择当前最佳的行动,以最大化即时或长期的奖励。与之相对的是“探索”,即尝试新行动以获取更多信息,有可能获取更好的长期奖励。
过于偏重利用,容易停滞在局部最优,减小找到更优行动可能性。过于偏重探索,会增加学习时间,延长模型收敛速度。
ε-Greedy 是平衡利用和探索的一种方法。
代理的边界
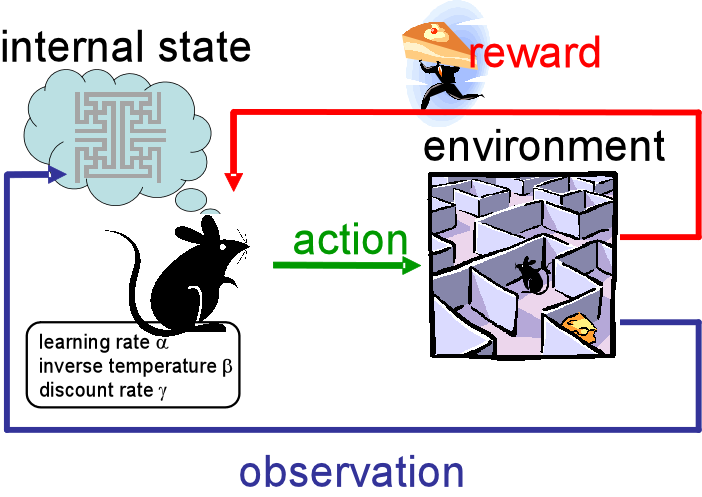
代理(Agent)是决策者或学习者,它根据当前的状态采取行动。代理的目标是学习一个策略(policy),即在给定状态下应采取什么行动以最大化累积奖励。使用奖励信号来贯彻这个目标是强化学习最明显的特征之一。
环境(Environment)是代理所处的世界,包含了代理可以感知的所有事物。它定义了代理可以执行的所有可能动作、所有可能的状态以及代理如何从环境中获得奖励。每当代理采取一个动作时,环境会返回一个新的状态,并且可能伴随着一个即时奖励(reward)信号,用来衡量该动作的好坏。
代理和环境的边界不一定是物理边界,一个代理的边界是它能完全控制的部分,一个机器人可能有多个代理,一个代理的环境可能包含了机器人的其它部分。比如一个回收机器人,它可能拥有多个代理,负责移动的代理、负责抓取空罐的代理、负责决策(何时搜索、待机、返回充电)的代理。
情节任务
情节任务或回合任务(Episodic Tasks)是强化学习中的一种任务类型,与持续任务(continuing tasks)相对。在情节任务中,代理在一个环境中执行一系列动作,直到达到某个终止状态,然后任务结束。每个完整的任务实例被称为一个“episode”(情节或回合)。比如在象棋中,一局对弈就是一个完整的情节或回合。